▪ماذا تعني الزاوية الصلبة رياضياً وفيزيائياً ؟

تُشكل الزاوية الصلبة في الفيزياء عائقاً أمام الكثير من الطلبة، لأنها أحياناً لا تكون واضحة وجلية للكثير مما يضطرهم الى حفظ تعبيرها الرياضي دون أن يفهم معناها فحواها الفيزيائي المهم للغاية.

سوف نبدأ أولاً بالأشياء البسيطة والتي تعرفتهم عليها في مستويات أدنى من قبل وعلى الخصوص بالمستوى الثانوي، وهي الزاوية العادية المعروفة والتي تعرفونها جميعكم والتي نرمز لها بالعديد من الرموز، لكن سوف نختار في حالتنا الرمز تيطا θ، والعلاقة بين الأفصول الزاوي θ والأفصول المنحني l على الدائرة المعروفة هي الأخرى وتكتب كالتالي:

l = r.θ (1)

حيث r هو شعاع الدائرة.

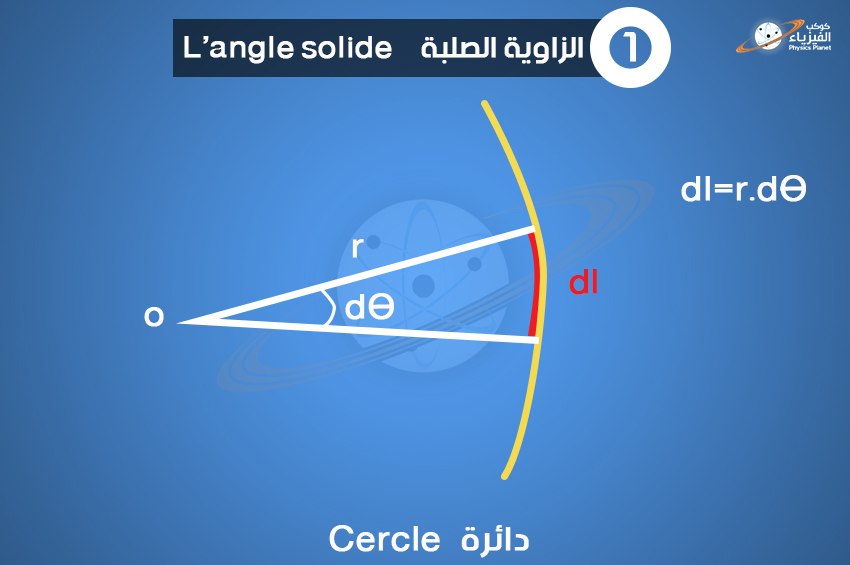
▪ماذا يعني الأفصول الزاوي θ في هذه الحالة من خلال الصورة أعلاه؟

الأفصول الزاوي θ يُمثل الزاوية التي نستطيع من خلالها رؤية قوس l الدائرة إنطلاقاً من المركز O.

وفي حالة إذا كان الأفصول الزاوي صغير جداً نعبر عنه بالتغير الجزئي وتكتب العلاقة (1) كالتالي :

dl = r.dθ

حيث dθ و dl تُمثل تغيرات صغيرة جداً للأفصولين الزاوي والمنحني.

في هذا التقديم كنا نتكلم فقط عن الدائرة، بحيث لم نكُن نحتاح إلا لبعد واحد لتحديد العلاقات التي تصفها رياضياً، لكن لنستبدل الآن الدائرة بفلكة أو كُرة كما توضح الصورة أسفله حيث نمثل فقط جزء صغير من الفلكة.

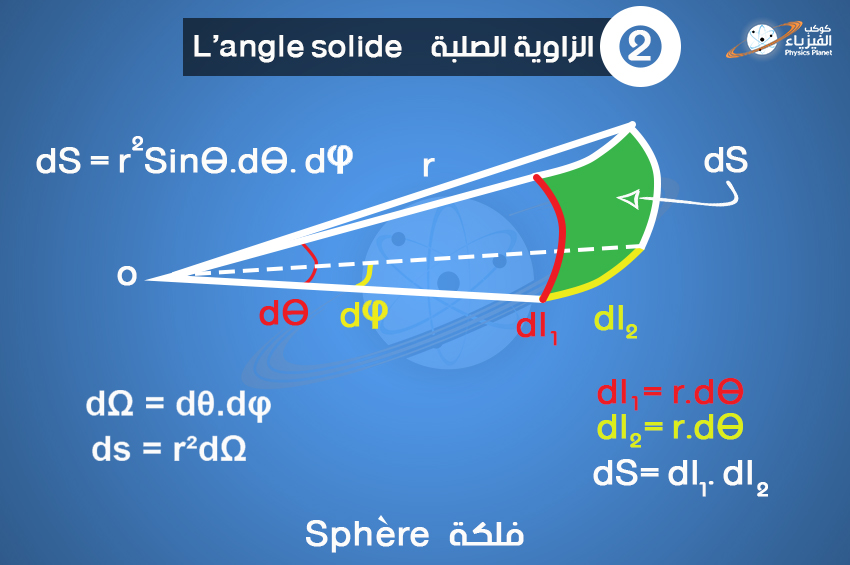
المساحة الجزئية للفلكة تُعطى بالعلاقة التالية والتي يُفترض أنكم تعرفون تعبيرها :

ds = r²sinθdθ.dφ

وهنا نرى كذلك أن dθ تُمثل الزاوية التي يُمكن من خلالها رؤية القوس العمودي dl₁ للدائرة الأولى و dφ الزاوية التي يمكن من خلالها رؤية القوس الأفقي dl₂ للدائرة الثانية، لكن إذا أخذنا الأفصول الزاوي dθ وضربناه في الأفصول الزاوي dφ، سوف نحصل على الزاوية التي يمكن من خلالها رؤية المساحة ds والتي تكتب :

ds = dl₁.dl₂ ( 2)

كل ما تتضمنه الزاوية الصلبة من معنى يوجد في الجملة السالفة الذكر! أي أن الزاوية الصلبة هي الزاوية التي يمكن من خلالها رؤية المساحة ds إنطلاقاً من المركز O، ولهذا فإننا لا نحتاج في حالتنا هذه التحرك فقط في أفصول زاوي واحد كما هو الحال مع الدائرة سابقاً، وإنما نحتاج التحرك على الأفصول الزاوي العمودي θ وفي نفس الوقت على الأفصول الزاوي الأفقي φ لكي نستطيع رؤية المساحة المقابلة لنا s ونحن نقف على المركز O.

الزاوية الصلبة كما سبق تعريفها إذن هي ضرب الأفصولين الزاويين dθ و dφ، ومنه يمكن كتابة تعبير الزاوية الصلبة كالتالي:

dΩ = dθ.dφ

إذن لنبحث عن التعبير المعروف للزاوية الصلبة Ω بدلالة المساحة s و شعاع الفلكة r :

لدينا من خلال (2) :

ds = dl₁.dl₂

وبما أن :

dl₁ = r.dθ
dl₂ = r.dφ

فإن :

ds = r²dθ.dφ

ولدينا :

dΩ = dθ.dφ

إذن :

ds = r²dΩ

وبالتالي نحصل على التعبير الجزئي المعروف للزاوية الصلبة :

dΩ = ds/r² (3)

لنحسب الآن كم هي قيمة الزاوية الصلبة لرؤية الفلكة ذات الشعاع r ككل إنطلاقاً من المركز، أي الزاوية الصلبة التي نرى من خلالها الفضاء ككل.

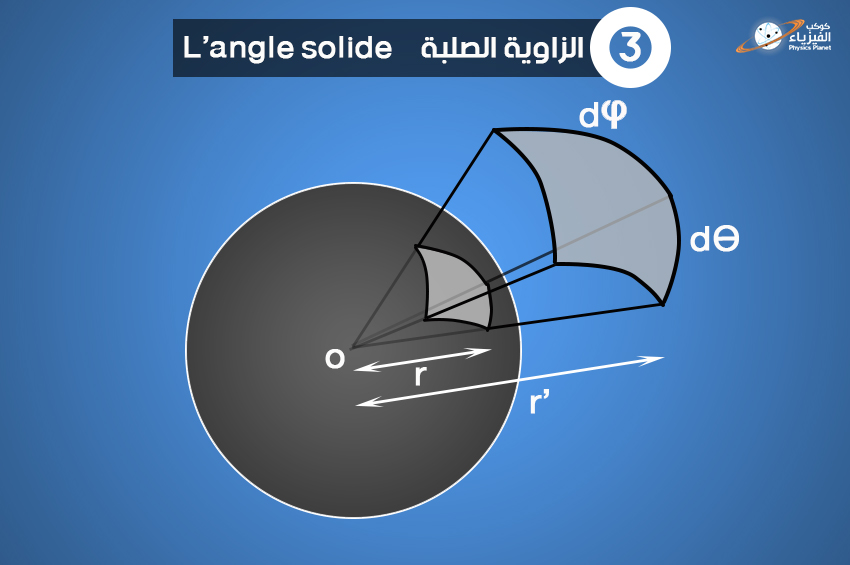
لدينا التعبير الجزئي للمساحة كالتالي :

ds = r²sinθdθ.dφ

نُعوض في العلاقة (3) فنحصل على :

dΩ = r²sinθdθ.dφ/r² = sinθdθ.dφ

نعطي مجال تغيُّر الأُفصولين الزاويين θ و φ :

θ∈[0;π] et φ∈[0;2π]

وبعد إجراء التكامل على المجالين :

Ω = ∫dΩ = ∬sinθdθ.dφ = – [cosθ]×[φ] = -[-1 – (1)].[2π] = 4π

ومنه :

Ω = 4π

إذن الزاوية الصلبة الكلية التي يمكن من خلالها رؤية كل الفضاء انطلاقاً من المركز O هي 4π.

الحالة التي قدمناها هنا للزاوية الصلبة هي حالة بسيطة حيث أنه إعتبرنا أن المنحى n الذي يوجه المساحة ds متوازي دائماً مع اتجاه المسافة r التي تفصله عن المركز O، ولهما نفس المنحى كذلك ، بمعني أنه في أي نقطة في المكان لدينا :

n = u

تجدر الاشارة هنا الى أن n و u عبارة عن متجهات واحدية لهما منظم يساوي 1.

وهذه الحالة التي أوردناها لا توجد إلا في حالة الفلكة التي قدمناها، أما في الحالة العامة فقد تكون المساحة التي نراها من المركز O ليست بالضرورة عبارة عن قطعة من فلكة، وبالتالي فلن يكون هناك توجيه دائم للمساحة متوازي مع اتجاه المسافة التي تفصله على المركز O، ومنه يجب استعمال الجداء السلمي من أجل الاسقاط، وسوف نورد مثال الزاوية الصلبة لرؤية مساحة قرص انطلاقاً من المركز.

التعبير العام يكتب باستعمال الجداء السلمي كالتالي :

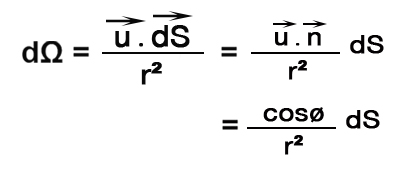
مع :

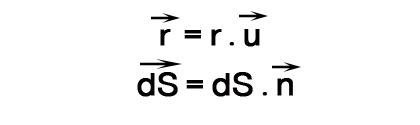
هذا التعبير نستعمله عندما لا يكون هناك توازي دائم بين منحى توجه المساحة n ومنحى توجه المسافة r.

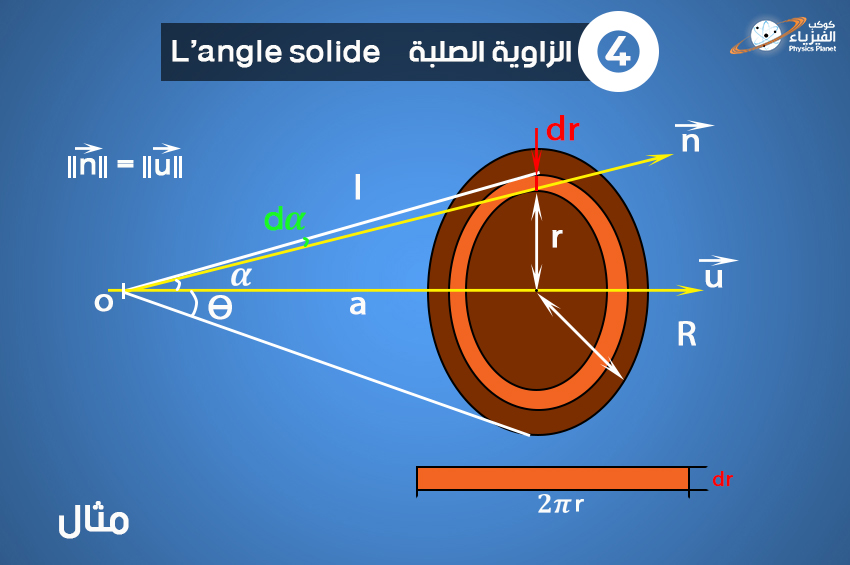
حساب الزاوية الصلبة لرؤية قرص شعاعه R انطلاقاً من المركز O.

حساب الزاوية الصلبة التي من خلالها نرى قرص شعاعه R.
لحساب الزاوية الصلبة للقرص المرئي من نقطة محوره o ، يجب علينا أولاً حساب الزاوية الصلبة الأولية dr التي من خلالها نرى حلقة أولية

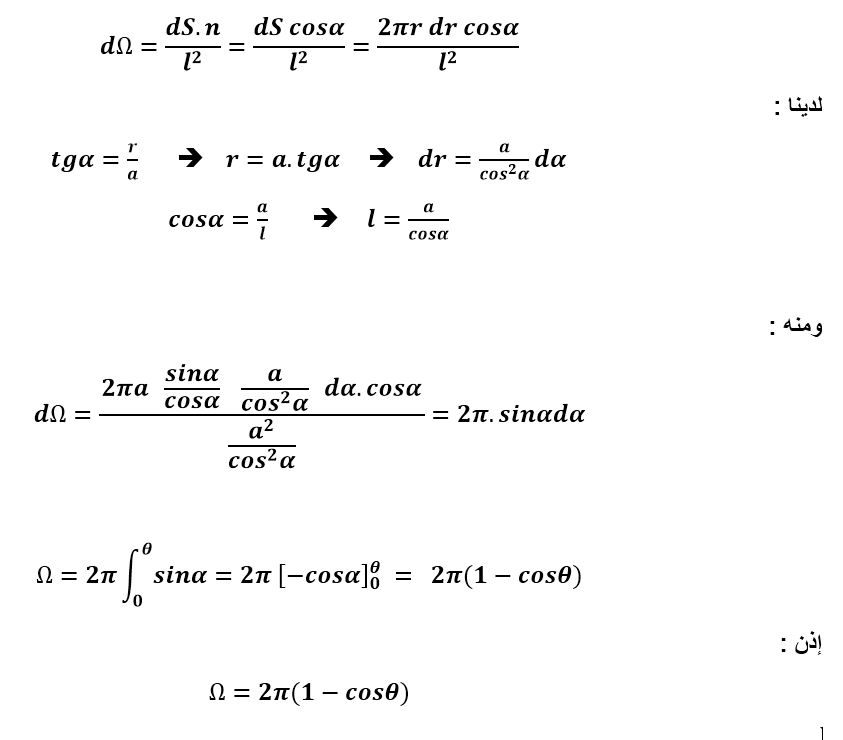
مثلا اذا كانت :

θ = π/3

Cos(π/3) = 1/2

ومنه :

Ω = 2π/2 = π

▪مصطلحات :

Angle solide : الزاوية الصلبة
Abscisse curviligne : الأفصول المنحني
Abscisse anglaire : الأفصول الزاوي
Variation élementaire : تغير جزئي
Sphère : فلكة

إعداد شعيب المستعين

مراجعة لغوية : نادية بوحفص

---

اقرأ أيضا :