توصلنا في الجزء الأول من هذا المقال إلى المتساوية التالية :

ℏω = p²/2m + V(r) (1)

وقلنا أنه من خلالها سوف نستطيع أن نبرهن على معادلة شرودينغر بالصورة أسفله، ويمكنك قراءة الجزء الأول من هذا المقال (ستجد الرابط أسفله).

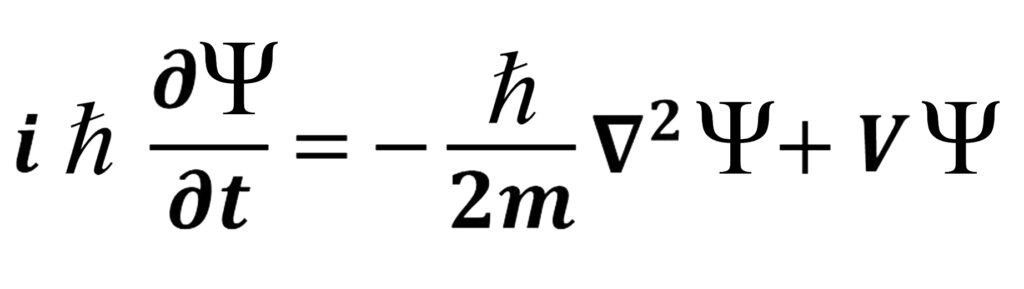
لدينا حسب مسلمة لويس ديبرولي والتي تكلمنا عنها كذلك في الجزء الأول كالتالي :
p = ℏk

نعوض ب p في العلاقة (1) فنحصل على :

ℏω =ℏ²k²/2m + V(r) (2)

بما أننا نعتبر أن الجسيمات اللانسبية هنا تتصرف كالموجات، سوف نفترض أن ψ هي دالة الموجة للجسيمات، ثم نضرب طرفي المتساوية السابقة في دالة الموجة هذه فنحصل على :

ℏωψ=ℏ²k²ψ/2m + V(r)ψ

قبل أن نستمر في البرهان يجب أن نذكر أولا بمعادلة الموجات المعروفة والمسماة ب “معادلة دالمبير” في بعد واحد وهي كالتالي :

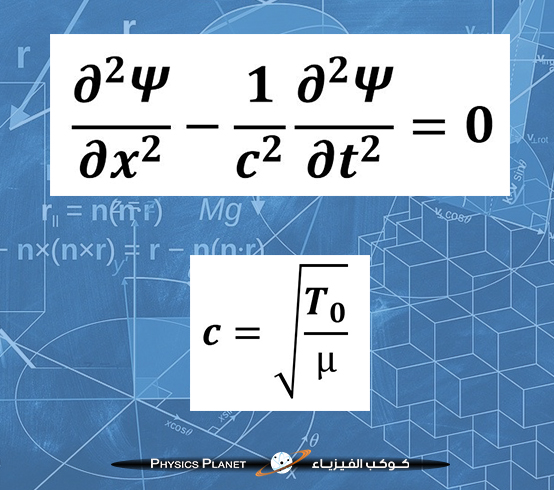
نعلم أنه عند المرور من المشتقات في المعادلة التفاضلية نحو علاقة التبدد فإننا نأخد معادلة إنتشار الموجات في الحالة المعقدة ومنه فإن حسب دالة الموجة المعروفة سواء في الموجات الميكانيكية أو في الموجات الكهرومغناطيسية فإن :

∂/∂t ——> -iω (a)

∂²/∂²t ——> -ω² (b)

∂/∂x ——> ik (c)

∂²/∂²x ——> -k² (d)

نعوض ب (b) و (d) في معادلة الموجات “معادلة دالمبير” فنحصل على علاقة التبدد التالية :

-k²ψ – (1/c²).(-ω²ψ) = 0

نختزل ب ψ من كلا الطرفين فنحصل على :
ω² = c²k²

وهذه العلاقة تسمى بعلاقة التبدد، فإذا ضربنا الطرفين في دالة الموجة ψ حيث أن هذه الدالة تتعلق بالزمان t والمكان r ، ورجعنا بالاتجاه المعاكس فإننا سوف نحصل على معادلة الموجات التي انطلقنا منها، وهذا ما سوف نفعله مع المعادلة (2) التي سبق وحصلنا عليها حيث سنعتبرها كعلاقة التبدد وعند ضربها في ψ حصلنا على :

ℏωψ(r,t)=ℏ²k²ψ(r,t)/2m + V(r,t)ψ(r,t) (3)

وهنا سوف نعوض كل من k² و ω في المعادلة لكي نحصل على المعادلة التفاضلية بالمشتقات حسب الزمان والمكان كما هو الحال مع معادلة الموجات “معادلة دالمبير” :

إذن لدينا من خلال (a) و (d) :

∂/∂t ——> -iω

∂²/∂²x ——> -k²

:ومنه فإن

ω ——> – ∂/i∂t

k² ——> – ∂²/∂²x

نعوض ω و k² بتعبيرهما في المعادلة (3) مع العلم أن الدالة تتعلق بالزمان t والمكان r وللإختصار سوف نظهر ذلك في المعادلة النهائية إذن :

-ℏ(∂/i∂t)ψ= (-ℏ²/2m) (∂²/∂²x)ψ + Vψ

وبإعادة ترتيب المتساوية نحصل على :

iℏ∂ψ(r,t)/∂t= (-ℏ²/2m)(∂²ψ(r,t)/∂²x) + V(r,t)ψ(r,t)

وهذه هي معادلة شرودينغر المشهورة !

حيث أن الهاميلتونيان H هو :

(e)
H = (-ℏ²/2m)∂²/∂²x + V

والطاقة E هي :

(f)
E = iℏ∂/∂t

لأنه كما نعلم :

∂/∂t ——> -iω

أي :
i.∂/∂t ——> ω

وبالتعويض في (f) نحصل على :
E =ℏω

وهذه هي المسلمة الخاصة بالطاقة الكلية للجسيم التي انطلقنا منها …

ومن خلال ( e) و (f) يمكن إختصار المعادلة كالتالي :

E.ψ = H.ψ

ويمكن أن نستنتج من خلال البعد الواحد لهذه المعادلة، المعادلة الاجمالية في الأبعاد الثلاثة إضافة الى الزمن، وذلك بتعويض المشتقة الثانية بدلالة المكان ب “لابلصيان” الذي يساوي مربع نابلة :

∆ = ∇²

فتصبح المعادلة كالتالي :

iℏ∂ψ(r,t)/∂t= (-ℏ²/2m)∆ψ(r,t) + V(r,t)ψ(r,t)

▪ملاحظة :

في الحقيقة معادلة شرودينغر في فيزياء الكم تقدم كمسلمة لا برهان عليها، لأنه حتى شرودينغر نفسه لم يُقدم أي برهان رياضي حقيقي يحترم كل ما هو رياضي وفيزيائي في البرهان، لأن دالة الموجة التي نتكلم عنها في المعادلة لا معنى فيزيائي لها وبما أن الأمر كذلك فلا يمكن أن نعلم ماهية الجسيم الحقيقية، دالة الموجة لا تمثل الآن في فيزياء الكم أكثر من أنها دالة رياضية لا معنى فيزيائي لها، ومربعها ψ|²| فقط هو من له معنى فيزيائي حيث يمثل كثافة إحتمال تواجد الجسيم في مكان ما، فدالة الموجة إذن تخضع لشروط رياضية وفيزيائية ولكن لا معنى فيزيائي لها.

▪مصطلحات :

Equation de D’Almbert : معادلة دالمبير
Equation de dispersion : معادلة التبدد
Postulat : مسلمة
Hamiltonien : هاميلتونيان
Laplacien : لابلصيان

إعداد : شعيب المستعين

المراجعة اللغوية : نادية بوحفص

---

إقرأ أيضا الجزء الأول :