يُعطى تعبير العدد الموجي k كالتالي :

k = 2π/λ

اذا لاحظنا وحدته من خلال التعبير نجد أنه rad/m !

لنعد أدراجنا الى التعبير الاصلي الذي يظهر فيه ، نأخد تعبير الموجة المستوائية والذي يكتب بصفة عامة كالتالي :

ψ(x,t) = A.cos(φ(x,t))

هذه الموجة تنتشر في بعد واحد وفق المحور ox .

حيث :

φ(x,t) = ωt – k.x

مع العلم أن كل من ω و k ثوابت !

وهذا التعبير الأخير يسمى بطور الموجة ، وهنا نلاحظ أنه على عكس ما تم التطرق إليه في المنشور الخاص بطور الذبذبات و الذي كنا نقتصر فيه على وجود ωt في الطور والذي كان يفسر وجود متذبذبات تتذبذب خلال الزمن في نفس المكان ، فإنه يلاحظ ظهور طرف جديد k.x والذي يعبر على أن هذه الذبذبات و التي هي عبارة عن موجات لم يعد يقتصر تذبذبها خلال الزمن في نفس المكان بل تذبذبات منتشرة في المكان كذلك .

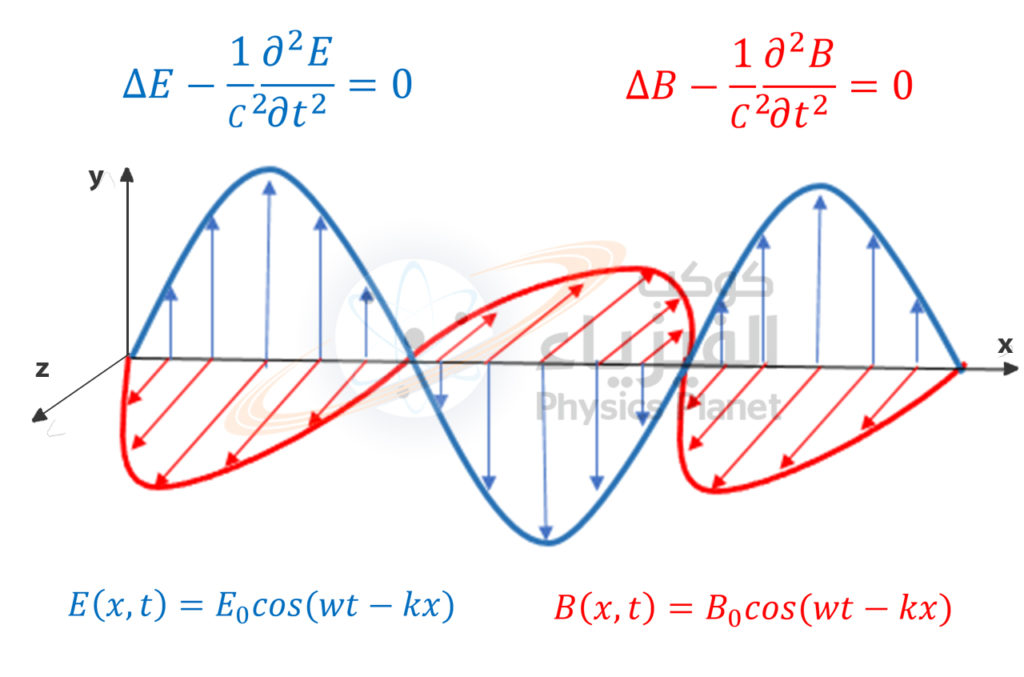
إذن ماذا يمثل هذا العنصر الجديد k الموجود في الطرف الإضافي في الطور ؟

كما يلاحظ هنا الطور لم يعد مرتبط فقط بمتغير واحد وانما مرتبط بمتغييرين اثنين هما الزمن t و المكان x ، وهما متغيرين غير مرتبطين فيما بينهما ، ولهذا فاشتقاق الطور هنا يتطلب أن يكون جزئي ، أي عندما نشتق الطور وفق متغير يجب أن نجعل المتغير الثاني ثابت .

• إذن لنشتق الطور اشتقاق جزئي بالنسبة للزمن مع ترك المتغير المكاني x ثابت فنحصل على :

∂φ(x,t)/∂t⌋ₓ = ω

وهنا نلاحظ كما سبق و أن تطرقنا في المنشور السابق الخاص بمفهوم النبض أن ω تمثل السرعة التي يتغير بها طور الموجة بالنسبة للزمن .

• والاشتقاق الجزئي الثاني يكون بالنسبة للمكان x مع ترك المتغير الزمني t ثابت فنحصل على :

∂φ(x,t)/∂x⌋t = -k

وهنا نلاحظ أنه يمكن أن نفهم معنى العدد الموجي k بنفس الطريقة التي فهمنا بها النبض ω ، فإذا كان النبض ω يمثل سرعة تغير الطور خلال الزمن فإن k لا تمثل الا تغير الطور خلال المكان .

تجدر الاشارة هنا الى أنه اشارة الناقص الموجودة في العلاقة لا تشكل عسرا في الفهم ، فيمكن التخلص منها لأنها تشير فقط الى أن الطور يتناقص بدلالة المكان ولهذا فمشتقة الطور عبر المكان سالبة !

اذا كان العدد الموجي k ثابت يمكن أن نحسب القيمة المتوسطة له بالطريقة التالية :

k = ∆φ/∆x

عندما تتحرك الموجة في المكان بمسافة طول الموجة فإن :

∆x = λ

ومنه فإن تغير الطور خلال هذه المسافة يكون هو 2π ، لأن الطول الموجي هنا يعتبر الدور المكاني وذلك كما فعلنا فيما سبق مع الدور الزماني T في المنشور الخاص بشرح مفهوم الطور ومنه نكتب :

∆φ = 2π

ومنه تصبح قيمة العدد الموجي كالتالي :

k = 2π/λ (1)

• هل هناك علاقة تربط بين النبض ω و العدد الموجي k ؟

سبق وأن برهنا في المنشور الخاص بالنبض أن :

ω = 2π/T (2)

: نقسم (2) على (1) فنحصل على

ω/k = λ/T (3)

لدينا العلاقة التي تربط بين طول الموجة و سرعتها :
λ = v.T

λ/T = v

: نعوض في العلاقة (3) فنحصل على

ω/k = v

ومنه فإن :
ω = k.v

بالنسبة للموجات الكهرومغناطيسية فإن سرعة الموجة هي c ، إذن نحصل على العلاقة الشهيرة التي تربط بين النبض ، العدد الموجي و سرعة الضوء .

ω = k.c

• خلاصة

بما أن الطور في حالة الموجة مرتبط بمتغيرين اثنين ، الزمان t و المكان x فإن سرعة تغير الطور تتعلق بهما معاً ، ومنه فإن النبض ω هو السرعة الزمانية التي يتغير بها الطور و العدد الموجي k هو السرعة المكانية التي يتغير بها الطور . بمعنى أن ω تمثل قيمة الزاوية بالراديان التي يتغير بها الطور في كل ثانية واحدة و k يمثل قيمة الزاوية التي يتغير بها الطور في كل متر واحد .

ويجب أن نشير هنا أن العدد الموجي k مثله مثل النبض ω ليس معرف الا بالنسبة للدوال الجيبية (cos ,sin) ، كما أن هذه الدوال الجيبية تقبل وصفين متشابهين ، وصف مرتبط بالزمن t والذي نتكلم فيه عن وجود النبض ω وكذلك وصف مرتبط بالمكان x والذي نتكلم فيه عن وجود العدد الموجي k ، وهذان الوصفان تربط بينهما علاقة التبدد التالية :ω/k = v

مصطلحات :

Onde plane : موجة مستوائية
Nombre d’onde : العدد موجي
Phase : الطور
Période temporelle : الدور الزماني
Période spatiale : الدور المكاني
Dérivée partielle : المشتقة الجزئية
Pulsation : النبض

• تحرير : شعيب المستعين

المراجعة العلمية :

• محمد كعب : أستاذ مبرز في مادة الفيزياء و الكيمياء
• اسماعيل علوي : أستاذ مادة الفيزياء و الكيمياء بسلك الثانوي التأهيلي
• حسام بنكروم : أستاذ مادة الفيزياء و الكيمياء بسلك الثانوي التأهيلي

• التدقيق اللغوي : نادية بوحفص

• تصميم الصور : رشيد هروس