• تقديم

الطور φ(t) وحدته “الراديان” والتي هي وحدة الزاوية ولهذا فوحدته تدل على أنه مجرد زاوية ، يستعمل كثيراً في الفيزياء وخاصة فيما يتعلق بالحركات المتذبذبة في الميكانيك أو في الكهرباء ، ويستعمل كذلك في الموجات ، لكن ما هو هذا الطور و هل من معنى فيزيائي له ؟

غالباً ما نجده في الفيزياء حيث يعبر عن ظاهرة فيزيائية متذبذبة ما ويكتب على الشكل التالي :

φ(t) = ω.t + φ₀

يوجد هذا الطور في الكتابة الرياضية التالية :

X(t) = Xm.Cos(ω.t + φ₀)

والتي نحصل عليها كحل رياضي للمعادلة التفاضلية التالية :

d²X/d²t + ω₀²X = 0

وهذه المعادلة نحصل عليها انطلاقاً من تطبيق بعض القوانين الفيزيائية كقوانين نيوتن مثلاً .

. وهو موضوع مقالنا الآن φ(t)  ما يهمنا من هذا التقديم هو الطور

في الحقيقة لنفهم معنى الطور و نفهم كيف بدأت القصة معه في الفيزياء يجب أن نأخذ بعض الأمثلة الفيزيائية وندرسها خطوة بخطوة .

• دراسة الظاهرة فيزيائياً

نأخذ مثلا متذبذب ميكانيكي على شكل نابض يوجد على سطح أفقي مشدود من طرف حامل مثبت الى جدار و في الطرف الآخر جسم صلب ذي كتلة m ، و للتبسيط نعتبر أن الإحتكاكات مع الهواء و السطح مهملة ، نزيح النابض من موضع توازنه نحو اليمين بمسافة Xm ونطلقه بدون سرعة بدئية ، فيبدأ هذا المتذبذب بالتأرجح يسارا ويميناً بين قيمتين حديتين Xm+ و Xm- خلال الزمن دون توقف . كما يوضح ذلك الشكل (c) و (d) في الصورة أسفله .

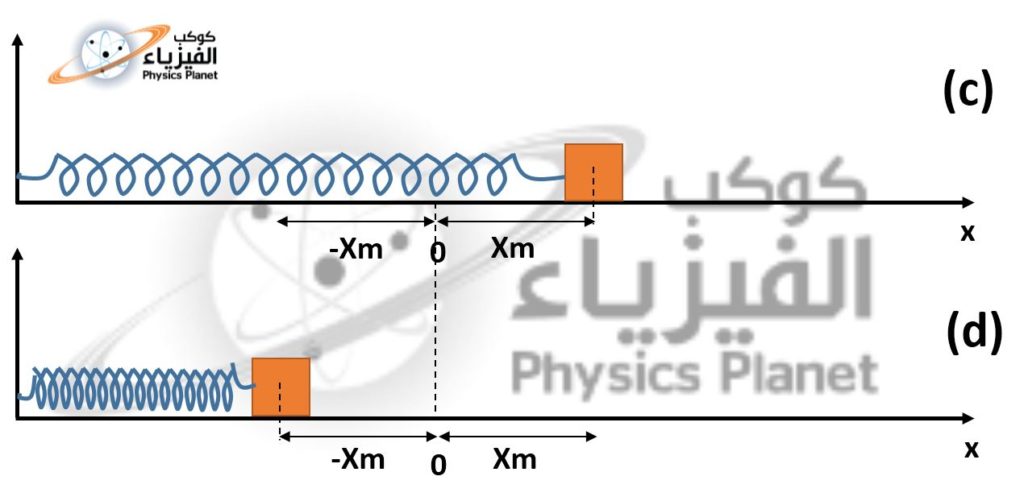
عندما نقول أن المتذبذب يتأرجح بين قيمتين حديتين  Xm+ و  Xm- لا يعني أنه لا يأخذ الا هاتين القيمتين بل هو يمر من كل المواضع المحصورة بين هاتين القيمتين الحديتين .

نعتبر أن

X(t) هو المتغير خلال الزمن الذي يأخد جميع القيم المحصورة بين Xm+ و Xm- ، إذن :

-Xm   ⩽  X(t)   ⩽  +Xm

و لكي نكون عمليين أكثر يجب أن ندرس هذه الحركة مبيانياً خلال الزمن لنرى كيف تتغير رياضياً المواضع X(t) خلال الزمن !

يبين الشكل (e) كيف يتغير الموضع X(t) مركز الكتلة الملتصقة بالنابض مع الزمن ، وهنا نرى بالضبط حركة دورية جيبية تتأرجح بين قيمتين حديتين Xm+ و Xm- ، شكلها يشبه تماماً شكل الدوال الجيبية (sinus , cosinus) ولهذا فيمكننا الاستعانة بهذه الدوال لكي نستطيع استخراج نموذج رياضي يحاكي نظرياً حركة المتبذبذب كما بيناه تطبيقياً في الشكل (e) بالصورة أسفله .

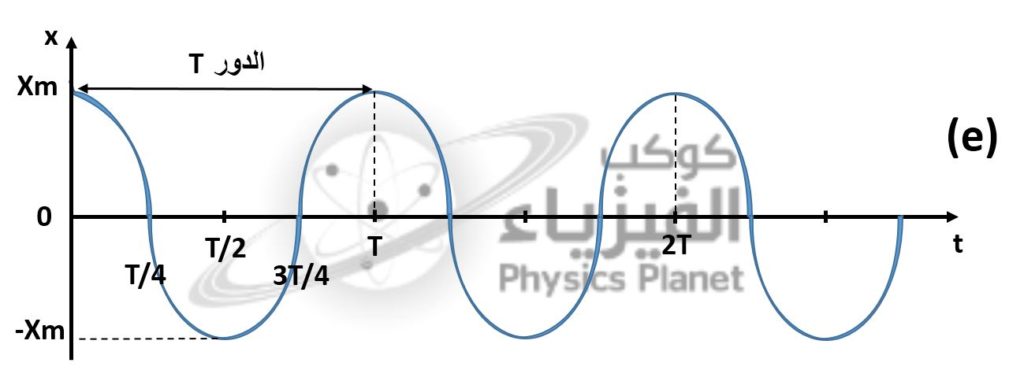
يتبين من خلال تغيرات X(t) بدلالة الزمن على الشكل (e) أن الحركة دورية دورها هو T ، أي أنه خلال مدة زمنية T تعيد الحركة نفسها . و من خلال المثال الذي ندرسه فالدور هو المدة الزمنية التي تحتاجها الكتلة الملتصقة بالنابض على اليمين لتذهب الى اليسار ثم تعود الى نفس مكانها البدئي على اليمين .

كما نلاحظ ذلك من خلال الشكل (e) أنه عند لحظات معينة يأخذ وسع الذبذبة X(t) قيم معينة :

نأخذ اللحظات التالية :

0   ,    T/4    ,    T/2    ,     3T/4    ,    T

 ونحسب قيمة وسع الذبذبة X(t) عند كل لحظة فنحصل على القيم التالية : 

X(0) = +Xm

X(T/4) = 0

X(T/2) = -Xm

X(3T/4) = 0

X(T) = +Xm

وهنا نلاحظ أنه عند اللحظة T و التي تشكل دور الظاهرة عادت الكتلة الى القيمة البدئية Xm .

• النمذجة الرياضية للظاهرة الفيزيائية

خلال هذه النمذجة الرياضية للظاهرة سوف نتصرف و كأننا لا نعلم شيء عن قوانين نيوتن أو عن المعادلات التفاضلية التي إنطلقنا من خلالها في التقديم ، بل سوف نجد النموذج المناسب دون حاجة الى ذلك و فقط باستعمال النمذجة الرياضية التي تعتمد على المحاكاة و المقارنة و التفكير الرياضي .

ما يهمنا هنا هو أن نجذ نموذج رياضي يحاكي بالضبط هذه النتائج التجريبية التي حصلنا عليها ، ومن خلال النتائج التي توصلنا اليها بعد دراسة الظاهرة الفيزيائية (المتذبذب الميكانيكي) تَبيَّن لنا أن النموذج الأصلح هو إستعمال دالة جيبية .

وهنا سوف نستعين بالدائرة المثلثية ذات الشعاع Xm ، لإستخلاص النموذج الرياضي المناسب للظاهرة الفيزيائية ، و كما تشاهدون في الصورة أسفله الشكل (a)  و (b) . نحاكي رياضياً حركة المتذبذب بالدوران على الدائرة المثلثية ونأخذ cosinus زاوية الدوران داخل المثلث القائم الزاوية فنحصل على :

Cosφ(t) = X(t)/Xm

ومنه :

X(t) = Xm.Cos(φ(t))    (1)

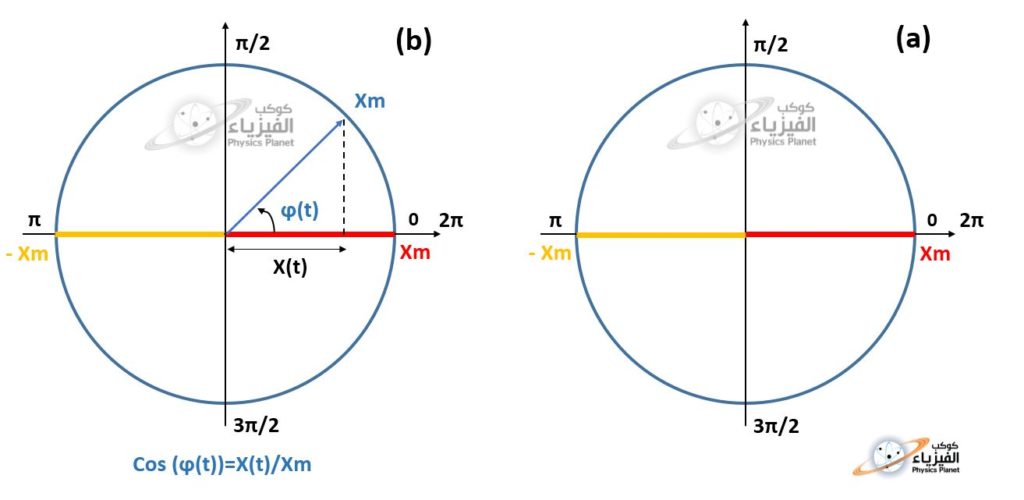
نعلم أن دالة cosinus محصورة بين القيمتين 1+ و 1- ولها نفس شكل الظاهرة الفيزيائية التي درسناها ومنه فضربها في Xm سوف يعطينا نتائج نظرية جد مطابقة للنتائج العملية التي حصلنا عليها من خلال القياسات التجريبية لدراسة الظاهرة الفيزيائية .

بما أن هذه الزاوية φ(t) تتغير بدلالة الزمن اذن توجد هناك سرعة تتغير بها هذه الزاوية خلال الزمن ، نضع ω هي سرعة تغير الزاوية بدلالة الزمن ومنه يمكن وضعها رياضياً على شكل مشتقة :

ω = dφ(t)/dt

نعتبر أن سرعة تغير الطور ثابتة :

ω = Δφ(t)/Δt  (2)

Δφ(t) = φ(t)  – φ₀

Δt = t – t ₀

نأخذ الزاوية عند الأصل φ ₀ غير منعدمة و نأخذ الزمن عند بدأ الحركة هي لحظة الصفر t ₀ = 0 ، ومنه نحصل على :

Δφ(t) = φ(t) – φ₀

Δt = t

فتصبح العلاقة مبسطة بالشكل التالي :

ω = (φ(t) -φ₀)/t    (3)

ومنه فإن :

φ(t) = ω.t + φ₀

: نعوض في العلاقة (1) فتصبح العلاقة كالتالي

X(t) = Xm.Cos(ω.t + φ₀)

الحركة على الدائرة المثلثية حركة دورية و دورها هو 2π أي أن الدور يمكن كتابته كالتالي :

φ(t) = 2π.m

حيث m يأخذ القيم : 0 ،1 ، 2 ، 3 ، 4 ، 5 ….

وهذا يظهر جلياً من خلال العلاقة :

Cosφ(t) = X(t)/Xm

لأن :

cos(2π.m) = 1

ومنه :

X(t) = Xm

 يعني أنه بعد كل دورة كاملة على الدائرة المثلثية يأخذ المتغير X القيمة الحدية القصوى Xm .

للتبسيط سوف نأخذ الطور عند الاصل φ₀ منعدم ، سوف نبدأ إذن من الزاوية صفر عند الأصل ثم نستمر في التعويض حتى نرى في أي زاوية سوف نعود الى نفس اللحظة البدئية ، ولهذا نأخذ القيم التالية ونعوضها في العلاقة :

φ(t) = 0    ,    φ(t) = π/2    ,    φ(t) = π     ,    φ(t) = 3π/2    ,   φ(t) = 2π  .

cos(0) = 1        ;     X(t) = Xm

cos(π/2) = 0    ;     X(t) = 0

cos(π)  = -1      ;     X(t) = -Xm

cos(3π/2) = 0  ;     X(t) = 0

cos(2π) = 0      ;     X(t) = Xm

نلاحظ هنا أننا بعدما أكملنا دورة كاملة أصبح X(t) يساوي Xm  وهي نفسها القيمة التي كانت عند الزاوية صفر مما يعني أن الحركة تعيد نفسها بعد مرور كل 2π .

• إذن ما هو الطور بعد كل هذه التفاصيل التي تطرقنا لها وما علاقته بالنبض ؟

النبض ω هو سرعة تغير الطور و لكن الطور كما رأينا من خلال النمذجة الرياضية للظاهرة الفيزيائية له مفهوم رياضي محض ، إذن فالطور له علاقة فقط بالنموذج الرياضي الذي تم اختياره ، ومنه فالنبض ω كذلك مفهومه رياضي متعلق بالنموذج نفسه ، لكن الرابط الوحيد الذي يجمع بين النموذج الرياضي و الظاهرة الفيزيائية هو الدور T أو التردد f ، فمدة اعادة تكرار الظاهرة الفيزيائية الدورية هي نفسها المدة الزمنية التي نحتاجها لانجاز دورة واحد على الدائرة المثلثية في النموذج الرياضي .

: لدينا من خلال العلاقة (3) باعتبار ان الطور عند الأصل منعدم

ω = φ(t)/t

خلال دورة واحدة تكون الزاوية هي 2π والمدة الزمنية اللازمة لانجاز دورة واحدة هي الدور T .

ومنه :

ω = 2π/T

وبما أن :

f = 1/T

فإن :

ω = 2π.f

حيث f هو تردد الحركة الدائرية في النموذج الرياضي وفي نفس الوقت تردد المتذبذب في الظاهرة الفيزيائية المدروسة .

• خلاصة

الطور φ(t) ليس له معنى فيزيائي هو مجرد ناتج نموذج رياضي يحاكي الظاهرة الفيزيائية المدروسة و نفس الشيء بالنسبة للنبض ω والذي يمثل تغير هذا الطور خلال الزمن . فالذي له مفهوم فيزيائيً وله علاقة وطيدة بالظاهرة الفيزيائية هو دور الظاهرة T للمتذبذب الميكانيكي و الذي يمثل أصغر مدة زمنية تتكرر خلالها الظاهرة ، و التردد f الذي يمثل عدد الذبذبات التي يقوم بها المتذبذب في كل ثانية .

تحرير : شعيب المستعين

مراجعة علمية :

• دريس لهبوب : أستاذ مبرز في الفيزياء و الكيمياء

• إسماعيل علوي : أستاذ الفيزياء و الكيمياء بالسلك الثانوي التأهيلي

التدقيق اللغوي : نادية بوحفص

تصميم الصور : رشيد هروس

تصميم الصورة المتحركة : ذ. عمر عسناوى