ذات يوم كان العالم العظيم ماكسويل جالساً في مكتبه يحتسي كوب من القهوة ويستمع الى برنامج خاص يبث في وقت محدد على المذياع ، ظل ماكسويل يتابع بانتباه البرنامج الى أن انتهى وبعد ان انتهى البرنامج أحس ببعض الملل فقرر أن يتسلى قليلاً بقوانين الطبيعة وبما أنه كان شخصاً يحب الرياضيات فقال لماذا لا أتسلى قليلاً بمعادلات المجال الكهربائي و المغناطيسي ، كتب القوانين و أخذ ينظر إليهم ثم لفت نظره قانون أُمير الذي ينص على أن غوطاسيونال المجال المغناطيسي rotB يساوي نفادية الفراغ μ0 ضرب كثافة التيار الكهربائي j :

rotB =μ0.j (1)

أمعن النظر قليلاً في هذا القانون وتذكر معادلة أخرى تتضمن كذلك كثافة التيار الكهربائي j وهي معادلة الشحنة :

Div(j) + dρ/dt = 0 (2)

وهو يعلم أن رياضياً :

div(rotB) = 0

فقال إذا قمت بإدخال div على قانون أمبير فإني سوف أحصل على تناقض بين القانونين :

div(rotB) =μ0.div(j) = 0

وهذا يكافئ أن :

div(j) = 0

لكن هذا ليس صحيحاً في المجال المتغير بدلالة الزمن لأن القانون يخرق مبدأ إنحفاظ الشحنة !

لأن حسب معادلة إنحفاظ الشحنة (2) فإن :

div(j) = -dρ/dt

وهذا يتناقض مع قانون أمبير لأن قانون أمبير يكون صالحاً فقط في حالة المجال الغير متغير بدلالة الزمن ، فاستنتج مباشرة أن قانون أمبير ينقصه شيء ما لأنه لا يحترم قانون إنحفاظ الشحنة الكهربائية !

فقرر البحث على هذا الطرف الذي ينقص قانون أمبير (1) :

فأضاف الى قانون أمبير المجهول x الذي ينقصه والذي يبحث عن قيمته فأعاد وكتب القانون في النظام المتغير بدلالة الزمن كالتالي :

rotB = μ0.j + x

ثم أدخل الديفرجونس div من جديد على المعادلة :

div(rotB) =μ0.div(j) + div(x)

وبما أنه لدينا رياضياً :

div(rotB) = 0

إذن :

μ0.div(j) + div(x) = 0 (3)

حسب معادلة إنحفاظ الشحنة (2) فإن :

div(j) = -dρ/dt

نعوض في المعادلة السابقة (3) فتصبح :

-μ0. dρ/dt +div(x) = 0

و لدينا حسب قانون كاوس :

div(E) = ρ/ε0

ρ = ε0.divE (4)

نشتق المعادلة (4) بدلالة الزمن فتصبح :

dρ/dt = ε0.(d(divE)/dt)

وبما أننا نشتغل في تقريب اوليريان وليس لاغراونجيان فالزمن منفصل على المكان إذن يمكننا أن ندخل مشتقة الزمن داخل الديفرجونس فتصبح المعادلة كالتالي :

dρ/dt = ε0.div(dE/dt)

ونعوض بالنتيجة في المعادلة (3) فتصبح :

-μ0.ε0.div(dE/dt) + div(x) = 0

يمكن إدخال μ0.ε0 داخل الديفرجونس لأنها مجرد ثابت فتصبح المعادلة كالتالي :

div(-μ0.ε0.dE/dt) + div(x) = 0

إذن :

div(-μ0.ε0.dE/dt + x) = 0

هذه المعادلة لها أكثر من حل لكنها تقبل كحل استثنائي وبسيط الحل التالي :

– μ0.ε0.dE/dt + x = 0

و هذا الحل هو الحل نفسه الذي إختاره ماكسويل للمعادلة .

إذن صديقنا الذي كان ينقص المعادلة هو :

x = μ0.ε0.dE/dt

ثم أضافه الى قانون أمبير فأصبح قانون أمبير في حالة النظام المتغير بدلالة الزمن يكتب كالتالي :

rotB = μ0.(j + ε0.dE/dt) = = μ0.(j + jd)

حيث أن :

jd = ε0.dE/dt

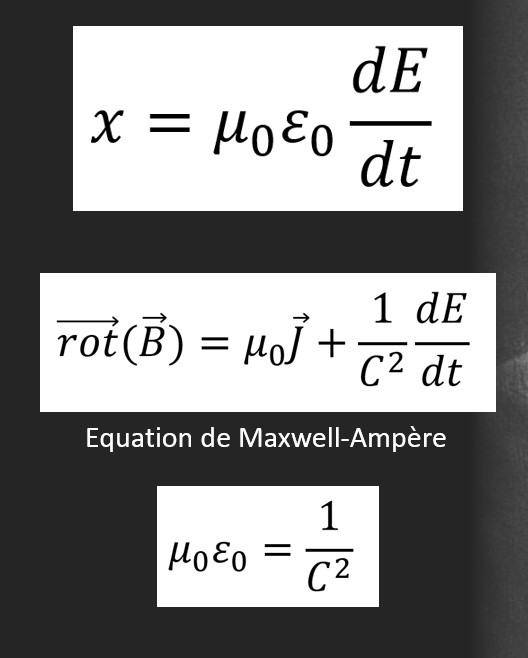
لكن هذا لم يكن في عهد ماكسويل الا حل نظري من أجل أن يُحترم قانون إنحفاظ الشحنة ، لكن فيما بعد سوف تؤكد التجربة التي قام بها هيرتز أن فعلاً تيار الانزياح هذا الذي اضافه مكسويل موجود .

وبذلك أصبح القانون يحترم مبدأ إنحفاظ الشحنة .

لقد سمى ماكسويل هذا الطرف الذي أضافه الى المعادلة بتيار الإنزياح jd .وبفضل هذا الإكتشاف العظيم وصل العالم الى ما وصل إليه حالياً فلولا هذا المجهول الذي اكتشفه ما كنت تستطيع قراءة هذا المنشور حالياً ، لأن بفضله تًم إكتشاف وجود الموجات الكهرومغناطيسية التي ساهمت فيما بعد في الاتصالات اللاسلكية و الانترنيت و الهواتف النقالة …

▪ ملاحظة
بخصوص القصة التي بدأت بها المقال هي مجرد قصة خيالية ، كما أنه في عهد ماكسويل لم يكن هناك شيء يسمى بالمذياع لأنه لم يكن حينها قد اكتشفت الموجات الكهرومغناطيسية ، كما أنه بفضل ماكسويل نستطيع اليوم الاستماع الى المذياع و مشاهدة التلفاز فهذا الإكتشاف البسيط جعل من العالم قرية صغيرة تتواصل فيما بينها في اجزاء من الثانية .

مصطلحات :

• تيار الإنزياح : Le courant de déplacement
• Rotationnel : rot
• Divergence : div

تحرير : شعيب المستعين