المسافة المكانية حسب قاعدة فيثاغورس في معلم ديكارتي ثلاثي الابعاد تكتب كالتالي :
(Δs)^2 = (Δx)^2 + (Δy)^2 + (Δz)^2 = r^2
كما تكتب في بعدين :
(Δs)^2 = (Δx)^2 + (Δy)^2
وفي بعد واحد :
(Δs)^2 = (Δx)^2
لكن عندما اكتشف اينشتاين ان الزمن الاحداثي t يتغير من مشاهد الى اخر لأن له ارتباط وثيق بالمكان وذلك عندما امعن النظر في تحويلات لورونتز وأخص بالذكر العلاقتين التاليتين :
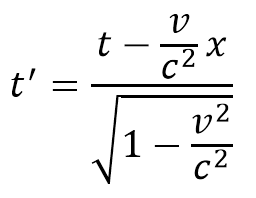
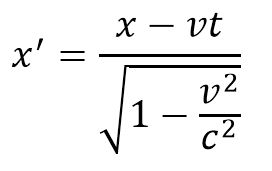
ومن هنا استنتج اينشتاين وجود بعد رابع يكون عموديا على الابعاد الثلاث المكانية التي نعرفها في المعلم الديكارتي ، لكن هذا البعد الرابع لا يمكن تمثيله بأي طريقة كانت بحيث يكون متعامد مع الابعاد المكانية الثلاثة ولهذا سوف نضعه في البعد التخيلي وليس مع الابعاد الحقيقية التي نستطيع تحسسها ورؤيتها.

ولهذا قرر ان يستعمل نفس العلاقة السابقة لفيثافورس التي تحدد المسافة المكانية في المعلم الديكارتي مع اضافة البعد الرابع وبذلك اصبح اسمها المسافة الزمكانية عوض المسافة المكانية :
(1)(Δs’)^2 = (Δx1)^2 + (Δx2)^2 + (Δx3)^2 + (Δx4)^2
حيث أن :
(2)Δx1 = Δx
Δx2 = Δy
Δx3 = Δz
Δx4 = ic.t
في حالة البعد الرابع يجب ان نضرب الزمن بالثابتة الكوني c الذي يمثل سرعة الضوء كي يكون هناك انسجام في الوحدات لأن c.t اصبحت تمثل مسافة في هذه الحالة وليست زمن! كما أنه يجب ضرب المسافة c.t في العدد التخيلي i لأن هذا البعد الرابع هو موجود في البعد التخيلي وليس الحقيقي لأننا لا نستطيع تمثيله في الواقع.
لنعوض اذن ب 1 في المعادلة 2 فتصبح العلاقة كالتالي :
(Δs’)^2 = (Δx1)^2 + (Δx2)^2 + (Δx3)^2 – (c.t)^2 = r^2 – (c.t)^2
لأن :
i^2 = -1
ملاحظة
قد إستعملت هنا الحرف s للتعبير عن المسافة وليس المساحة كما عهدناه ، حاولت فقط احترام الرموز الجاري بها العمل .
تحرير : شعيب المستعين







