كيف وجد نيلز بوهر مسلمته الشهيرة التي حل بها لغز إشعاع ذرة الهيدروجين و بنى عليها نموذجه في النظرية الخاصة بتكميم الطاقة في الذرة ، النموذج الذي كان له الأثر الكبير في ظهور ميكانيك الكم و صبر أغوار المادة و الذرة .
مسلمة نيلز بوهر تكتب كالتالي :
m.v.r = n.h/2π
من جملة المفاهيم و القوانين التي إنطلق منها بوهر في وضع مسلمته ، نظرية ماكس بلانك في تكميم الطاقة الصادرة عن إشعاع الجسم الأسود و العزم الحركي للجسيمات :
▪أولاً : نظرية ماكس بلانك لتكميم الطاقة الكهرومغناطيسية الصادرة عن الجسم الاسود .
لحل الكارثة التي كانت تحل بتفسيرات إشعاع الجسم الأسود إفترض ماكس بلانك أن الطاقة التي يشع بها الجسم ليست مستمرة كما إعتقد بعض العلماء الذين سبقوه الى تفسير هذا الأخير ، و إنما تنبعث على شكل كمات من الطاقة بشكل منفرد ، قيمة الكم الواحد يساوي h.f و يختلف هذا الكم من تردد إلى آخر ، و أعطت هذه الفرضية أُكلها و فسَّرت إشعاع الجسم الأسود بشكل دقيق يوافق التجربة و الملاحظة وكانت فرضية تكميم الطاقة التي إقترحها كالتالي :
En = n.h.f = n.E
E = h.f (1)
حيث n هو مكمم الطاقة و هو عبارة عن عدد صحيح و E هي أصغر كمية من الطاقة لتردد معين f و h ثابت بلانك .
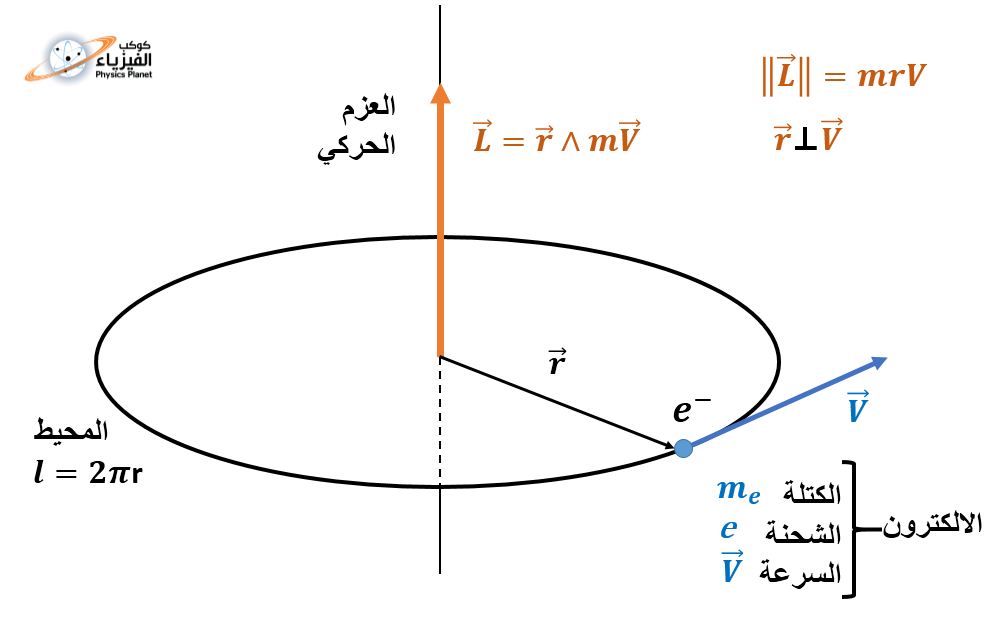
▪ثانياً : العزم الحركي للجسيمات في حالة دوران .
L = p.r = r.m.v (2)
p = m.v
حيث أن L هو العزم الحركي لجسيم في حالة دوران حول محور ثابت و r المسافة التي تفصله عن محور الدوران و v سرعته و m كتلته . p يمثل كمية حركة الجسيم .
انطلاقاً من (1) :
E = h.f = h/T
لأن التردد هو مقلوب الدور :
f = 1/T
ومنه :
h = E.T
يتبين إذن أن وحدة (الثابت) h هي : j.s
[h] = [E].[T] = j.s
ومن خلال (2) يتبين أن وحدة العزم الحركي هي كذلك j.s :
[L] = [p].r
لدينا حسب القانون الثاني لنيوتن :
F = dp/dt
dp = F.dt
ومنه :
[p]= [F].[t] = N.s
لنعوض في (3) فنحصل على :
[L] = [p].[r] = N.s.m = (N.m).s = j.s
ومنه فإن ثابتة بلانك h و العزم الحركي L لهما نفس الوحدة مما يدل على أن h تمثل قطعة صغيرة تكمم العزم الحركي L للجسيمات ! وهذا ما دفع نيلز بوهر إلى البحث على علاقة تكميم تجمع بين أصغر وحدة كمية للعزم h و العزم الحركي للجسيمات L .
كانت التفسيرات التي لم تأتي بأُكلها تعتبر أن الالكترون عند دورانه حول النواة لابد أن يشع طاقة كهرومغناطيسية و السبب أنه في حالة دورانه فإن متجهة سرعته تغير اتجاهها وهذا سوف يجعل الالكترون متسارعاً ومنه ضرورة انبعاث طاقة كهرومغناطيسية حسب الفيزياء الكلاسيكية ، لكن هذا كان يتنافى مع التجربة و الملاحظة لأنه لو كان هذا الأمر صحيحا لتطلب ذلك سقوط الالكترون على النواة في حركة حلزونية لأن اشعاع الطاقة سيجعل طاقته الكلية تتناقص و منه استنزاف طاقته وسقوطه على النواة و هذا سوف يؤدي بالضرورة إلى انهيار المادة بشكل عام الشيء الذي لم يكن يحدث في الحقيقة .
ولهذا أتى نيلز بور بفكرته الثورية و التي استوحاها بناء فقط على انسجام الوحدات كما سبق و أن بيناه ، فقال أن كمية حركة الالكترون p ضرب المسافة التي يقطعها خلال دورانه l ، لابد و أن تساوي ثابت بلانك h ضرب المُكمم n ، وهذا فقط إستنتاج مباشر من إنسجام وحدتيهما .
أي أن :
l.p = n.h
حيث l هو المسار الدائري الذي يدور فيه الالكترون حول النواة :
l = 2π.r
و p كمية حركة الالكترون عند دورانه حول النواة :
p = m.v
يجب أن نلاحظ أن l.p لها نفس وحدة h والتي هي j.s كما سبق و أن بين ذلك …
ومنه فإن :
l.p = 2π.r.m.v = n.h
إذن :
m.v.r = n.h/2π
وها قد وصلنا أخيراً إلى ما وضعه نيلز بوهر كمسلمة دون أن يضع له أي برهان …
من خلال هذه المسلمة التي طرحها بوهر لحل مشكل إنهيار المادة الذي كان في النماذج السابقة التي قدمها علماء آخرون ، إستطاع أن يفسر إشعاع ذرة الهيدروجين بطريقة جد دقيقة و تتوافق بشكل رائع مع التجربة ، وكان هذا الفرض يتطلب أن لا يشع الالكترون أي طاقة كهرومغناطيسية إذا ما إستمر في الدوران على نفس المدار ، لأن الإشعاع أصبح مرتبط فقط بقفزات الالكترون من مدار الى آخر .
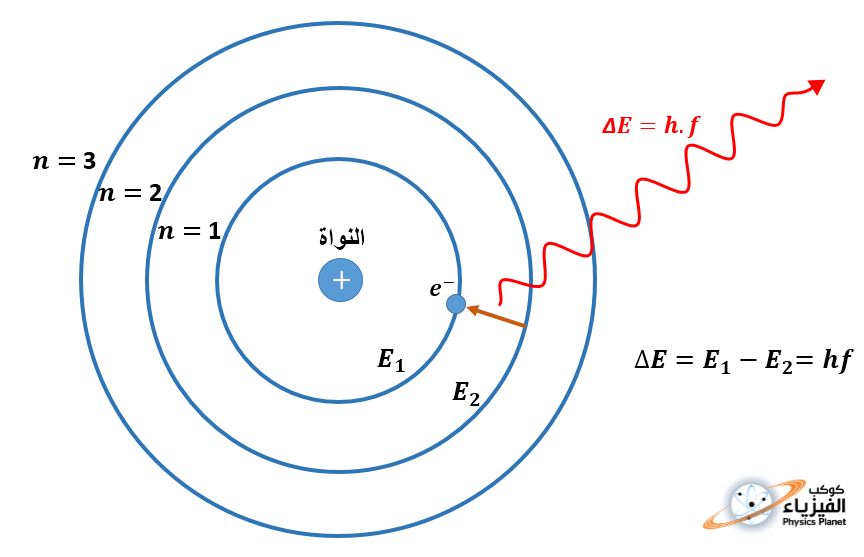
▪ملاحظة:
تجدر الإشارة هنا إلى أن هذا البرهان هو فقط إجتهاد شخصي ، لأنه لا توجد أيَّة مصادر تبين كيف وجد نيلز بوهر مسلمته الشهيرة هذه ، كما أن أغلب المصادر تذكر فقط أن نيلز بوهر لم يضع لها أي برهان ، و لهذا السبب تسمى مسلمة لأنها بدون برهان رياضي … كيف وجدها؟! لا ندري ، لكن اجتهدنا لكي نعرف ماذا كتب نيلز بوهر في وساخه وكيف خمن حتى كانت هذه المسلمة تعطي أُكلها في تفسير إشعاع ذرة الهيدروجين .
▪مصطلحات
Moment cinétique : عزم حركي
Quantité de mouvement : كمية الحركة
Quantification : تكميم
إعداد : شعيب المستعين
مراجعة لغوية : نادية بوحفص و خولة سطيلي
مراجعة علمية :
حسام بنكروم و إسماعيل علوي
تصميم الصور : رشيد هروس






One Comment
مقال رائع وغني بارك الله فيك. أشير فقط إلى خطأ لغوي بحجم الإلكترون ههه نقول سبر الأغوار وليس (صبر الأغوار) تحية 🙏