• هل نستطيع رؤية كل الأشياء صغيرة القد بالمجهر الضوئي ؟

مجال رؤية الانسان محدود ليس فقط لأننا لا نستطيع رؤية بعض الأطياف الكهرومغناطيسية ، ولكن لأن بعض الأشياء المجهرية لا يمكن للعين المجردة رؤيتها مباشرة ، كمثال على ذلك الخلايا و الجراثيم و الفيروسات . ولهذا نضطر الى استعمال بعض الاجهزة المتطورة لتساعدنا على رؤية مثل هذه الاشياء المجهرية ، كالمجهر الضوئي مثلا ، الدور الذي يقوم به هذا المجهر هو قدرته على التقاط أكبر كمية ممكنة من الضوء الصادرة على ذلك الشيء المجهري وتكبير صورته ألاف المرات حتى تستطيع العين رؤيته بوضوح أو التقاط صورة له بواسطة كاميرا .

لكن هذا المجهر الضوئي له هو الآخر حدود فلا يمكنه مثلاً أن يجعلك ترى الذرة ، الالكترون ، البروتون و النوترون … لكن ما هو السبب الذي يجعل من هذا المجهر الضوئي غير قادر على إعطاء صورة لهذه الاشياء الصغيرة جداً التي ذكرناها ؟

يجب أن نعلم أولاً أن الضوء عبارة عن موجة كهرومغناطيسية ، تتميز بطول موجي وهذا الطول الموجي هو المسافة التي تقطعها الموجة في مدة زمنية جد صغيرة تسمى بدور الموجة ، كما أن الضوء يمكنه أن يتصرف كذلك كجسيم حسب فيزياء الكم . الطاقة التي يحملها الفوتون تتعلق بتردده واذا قلنا التردد فإننا نقول ضمنيا كذلك تعلقه بالطول الموجي حسب العلاقة التالية :

E = h.f

لدينا العلاقة التي تربط الطول الموجي بالتردد كالتالي :

λ = c/f

حيث c هي سرعة الضوء .إذن :

E = h.c/λ

ومنه نلاحظ أن طاقة الفوتون متناسبة عكسياً مع الطول الموجي مما يعني أنه كلما أصبح الطول الموجي للفوتون أصغر كانت طاقته أكبر .

نعود الى طرحنا السابق ، لماذا للمجهر الضوئي حدود ! لأنه من شروط انعكاس الضوء على جسم معين أن يكون قَدُ (طوله d) ذلك الجسم أكبر من أو يساوي الطول الموجي λ للضوء المنعكس عليه .

أي أنه يجب أن يكون :

d ≥ λ

لنعطي رتبة قدر كل من الذرة و الالكترون مقارنة مع الطول الموجي للضوء :

رتبة قدر الذرة هي تقريباً :

d₂≈10⁻¹⁰ m

رتبة قدر الالكترون هي تقريباً :

d₁ ≈ 10⁻¹⁵ m

لكن الطول الموجي للضوء المرئي بالعين محصور بين 400nm و 800nm تقريباً أي أنه :

λmin = 4.10⁻⁷ m

λmax = 8.10⁻⁷ m

إذن :

λmin >> d₁ و d₂

λmax >> d₁ و d₂

ومنه يتبين أن قدُ (طول) هذه الجسيمات (ذرات ، الكترونات …) صغير جداً مقارنة مع الطول الموجي للضوء المرئي و لهذا فلا يمكن للمجهر الضوئي أن يعطينا صورة لهذه الأشياء التحت مجهرية . الضوء يمر على مثل هذه الجسيمات الدقيقة دون أن ينعكس عليها ، فهو يمر عليها وكأنها غير موجودة أمامه أصلاً .

• ما هو الحل اذن لرؤية هذه الجسيمات الدقيقة ؟

كان الحل امام العلماء هو استعمال موجات ذات طول موجي قصير جداً وقريب من طول هذه الجسيمات ، ثم يتم استعمال آليات أخرى لترجمة هذه الاشعة المنعكسة الى صور ، لأن هذه الاشعة سوف تكون خارج مجال رؤية الإنسان !

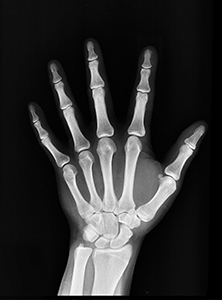
وقع الاختيار على الاشعة السينية (أشعة X) ذات الطول الموجي القصير و التي لا تدخل في الطيف المرئي من طرف العين ، هذا النوع من الاشعة هو الذي يستعمل في الميدان الطبي لتصوير الكسور التي تحدث على مستوى العظام ، لأن هذا النوع من الأشعة يستطيع اختراق اللحم دون أن ينعكس عليه . لكن هذه الاشعة لا تستطيع اختراق العظام بل تنعكس عليها مما يسمح للأطباء بالتقاط صور للعظام .

رتبة قدر الطول الموجي للأشعة السينية هي :

λ ≈ 10⁻¹¹ m

المشكل الذي وجده العلماء أن هذا النوع من الأشعة له طاقة عالية جداً ، لأن له طول موجي قصير كما سبق وأن فسرنا ذلك على كيفية ارتباط طاقة الفوتونات بالطول الموجي ، وهذا سوف يخلق مشكلة أخرى لدى العلماء .

المشكل الذي سوف يطرح هنا هو أن الضوء في حالة الموجات القصيرة يصبح تصرفه شبيه بالجسيمات لأن طاقته تصبح كبيرة ، لقد اختار العلماء موجات كهرومغناطيسية بطول موجي قريب من طول الذرة أو الالكترون لكي ينعكس عليهم ، لكن مشكل تصرف الضوء كجسيم سوف يجعل من هذا الانعكاس اصطدام بين جسيمين ، والذي هو جسيم الضوء مع الالكترون مثلا ، وهنا يكمن المشكل الحقيقي . ما كنا نتوقعه لن يحدث لأننا سوف نحصل فقط على اصطدام الشيء الذي سوف يجعل الالكترون يكتسب كمية حركة بعد سقوط اشعة X عليه (فوتون) .

و هنا سوف نصطدم مع أهم مبدأ في ميكانيك الكم《مبدأ عدم التحديد》 لهازينبرغ، الذي ينص على أنه من الناحية الكمومية الجسيمات الكمية ليست مُموضعة، بل هي تتصرف كموجات تشغل حيز من الفضاء على شكل حجم في نفس اللحظة، ولهذا لا يمكننا أن نقرنها بموضع نستطيع تحديده كما هو الحال في الميكانيك الكلاسيكية، هذا المبدأ الكمي ينص على أن عدم التحديد في الموضع للجسيم الكمي ضرب عدم التحديد في كمية حركته دائماً يكون أكبر من أو يساوي ثابت بلانك h.

لكن دعنا الآن أن نكون أقرب إلى الميكانيك الكلاسيكية ونفترض أن الإلكترون يمكنه أن يمتلك موضع معين، فهذا الإفتراض هو من أجل التبسيط لتقريب المفهوم فقط، فهنا مبدأ 《عدم التحديد》في ميكانيك الكم سوف يصبح على شكل 《مبدأ الإرتياب》 في الميكانيك الكلاسيكية، بحيث أنه يمكن أن نقرن بتحديد كمية الحركة وموضع الالكترون إرتياب يتغير بطريقة عكسية لكل من موضع وكمية حركة الالكترون، بحيث أنه كلما زادت الدقة في تحديد موضع الجسيم تضاءلت الدقة في تحديد كمية حركته. لأننا عندما نرسل أشعة X على الإلكترون تصطدم معه وتكسبه سرعة قبل أن تعود منعكسة الى المُستقبل، الشيء الذي يجعل صورة الالكترون المحمُولة من طرف الفوتون غير حقيقية، لأن الإلكترون قد تحرك من مكانه بفعل الإصطدام مع الفوتون.

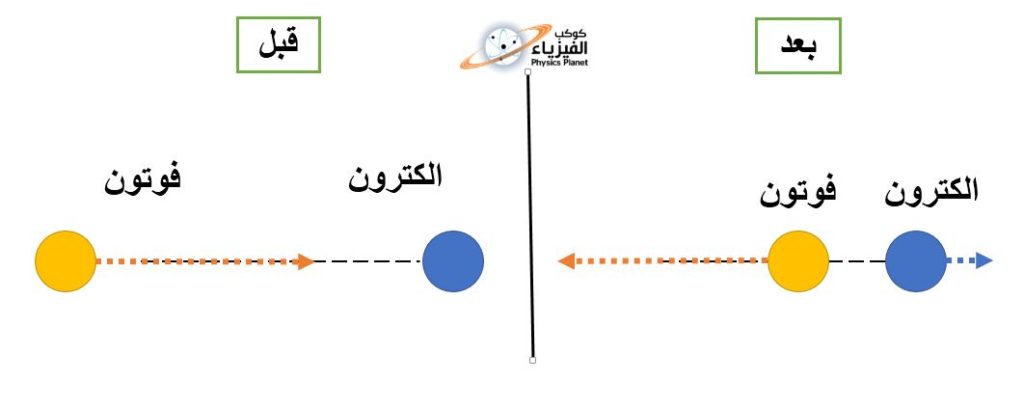
نلاحظ هنا أنه كلما كان الطول الموجي للاشعة قصير كانت طاقته أعظم، مما سوف يكسب الإلكترون طاقة كبيرة، الشيء الذي سوف يزيد من سرعته ومنه نقصان في دقة تحديد موقعه، و إذا أردنا أن نحدد موقعه بدقة أكبر وجب استعمال أشعة ذات طاقة أقل ومنه طول موجي أكبر إذن سوف نعود الى نفس المشكلة التي إنطلقنا منها وهي أن الطول الموجي للأشعة سوف يكون أكبر من طول (قَدُ) الإلكترون.

• خلاصة

لكي نعرف موضع الإلكترون يجب أن نستعمل طول موجي كبير للأشعة الكهرومغناطيسية، الشيء الذي ينتج عنه ازدياد في سرعة الجسيم عند الإصطدام، ومنه فقدان الدقة بشأن موضع الالكترون، وهنا نسقط في فخ أنه عوض أن نعرف مكانه بدقة نزيد في سرعته بسبب الإصطدام مع الفوتون ذو الطاقة الكبيرة. ولكن إذا ما أردنا أن نعرف سرعته بدقة يجب أن نقلل من طاقة الفوتون الساقط عليه ومنه استعمال طول موجي كبير للفوتون ومنه فقدان الدقة بشأن موضع الالكترون، لأن أغلب الفوتونات سوف تمر على الجسيم دون أن تنعكس عليه.

مصطلحات :

• Ordre de grandeur : رتبة قدر
• Dimension : ُقَد
• Microscope optique : مجهر ضوئي
• Rayon X : أشعة إكس
• Principe d’incertitude : مبدأ عدم اليقين

تحرير : شعيب المستعين Choaib El Moustaine

التدقيق اللغوي : هجر الناصيري ، نادية بوحفص .