هذا الجزء له علاقة وطيدة بالجزء الأول ولهذا قبل أن تبدأ في قراءته أنصحك بقراءة الجزء الأول .

▪ما هي علاقة الثابت π بالزوايا ؟

نعلم ان محيط الدائرة هو C=2.π.R اذا بدأنا الدوران من الزاوية °0 على الدائرة الى الزاوية °360 تكون المسافة المقطوعة هي محيط الدائرة C .

اذن يمكن كتابة التالي :

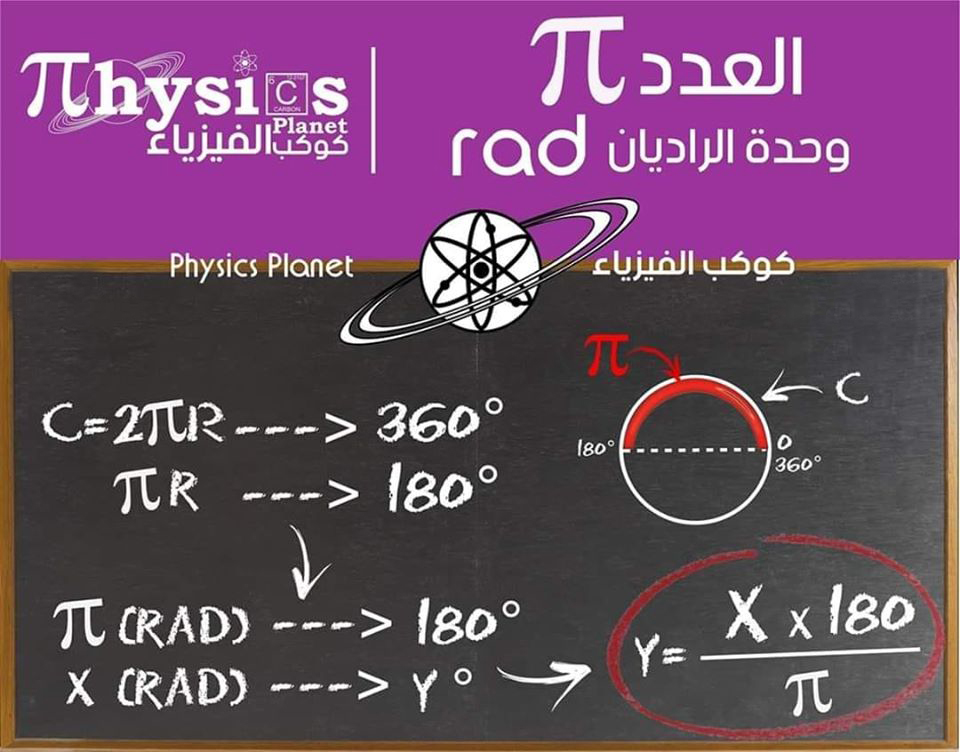
C=2.π.R ————> 360°

اذا قسمنا الطرفين على 2 ، يعني نصف محيط الدائرة تصبح الزاوية هي °180 اذن:

2.π.R/2 ————-> 360°/2

π.R ————–> 180°

نستطيع ان نأخد علاقة التكافؤ هذه لنبرهن على علاقة π بالزوايا .

لدينا اذن :

π.R ———> 180°

نلاحظ من خلال علاقة التكافؤ هذه بين طول القوس والزاوية °180 أنه كيفما كانت قيمة الشعاع R فلن تغير شيء في العلاقة لأن الزاوية بالدرجة تبقى هي نفسها!

الى هذه اللحظة لا يمثل π الا ثابت بدون وحدة كما بيناه في الجزء الاول ، اذن لنبحث عن كيفية اقحام وحدة الراديان لهذا الثابت ليستغل في حساب الزوايا.

كما قلنا فيما سبق ان الشعاع لا يؤثر في علاقة التكافؤ هذه ولكي لا نضطر في كل لحظة الى قول “π ضرب الشعاع” تكافئ °180 سوف نعوض الشعاع R بالقيمة 1 لنتخلص منه ونعطي للقيمة π وحدة الراديان “rad” في اشارة الى الشعاع radius بالانجليزية اذن تصبح العلاقة السابقة كالتالي:

π ————-> 180°

اذن كيفما كانت قيمة الشعاع R فإن القيمة π راديان تكافئ 180 درجة .

ف °180 تعني الزاوية بالدرجة و π تعني الزاوية بالراديان .

واذا ما اردنا ان نحول من الرديان الى الدرجة او العكس نستغل هذه العلاقة:

π (rad) ——–> 180°
x (rad) ——–> y°

y° =180°.X (rad)/π (rad)

بعد ان برهنا على علاقة π بالزاويا سوف نبين العلاقة التالية:
S = R.θ

حيث S يمثل فقط جزء من محيط الدائرة و R شعاعها و θ تمثل الزاوية بالراديان التي يحدها القوس S.

لذينا حسب العلاقة :
C = 2.π.R

اذن :
C/2 = π.R

حيث C/2 يمثل نصف قوس الدائرة.

إذا قسمنا الطرفين على 2 تصبح العلاقة:
C/4 = (π/2).R

حيث C/4 يمثل ربع محيط الدائرة و π/2 تمثل 90 درجة.

ونستمر هكذا نقسم من جديد الطرفين على 2 :

C/8 = (π/4).R

نلاحظ من خلال العلاقة ان الشعاع R لا يتغير وان المتغيرين الوحيدين في العلاقة هما الزاوية بالراديان وطول قوس الدائرة واذا ما استطعنا معرفة احد المتغيرين نستنتج منه الآخر باستعمال العلاقة ومنه لنعمم العلاقة بتعويض طول القوس بمجهول رمزه S والزاوية بمجهول آخر رمزه θ فتصبح العلاقة التي تربط طول قوس بالزاوية والشعاع كالتالي:
S = θ.R

ما لا يجب ان ننساه انه في هذه العلاقة π تعتبر فقط ثابتة بدون وحدة وذلك حسب العلاقة الاولى التي انطلقنا منها وبينها في الجزء الاول:

C = 2.π.R

تحرير : شعيب المستعين